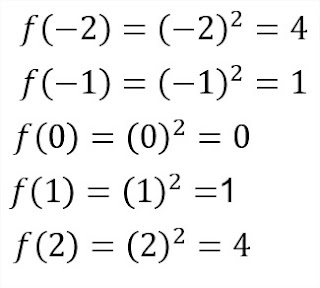El cálculo es una herramienta indispensable, pues nos permite desarrollar destrezas algebraicas que podemos aplicar y ver sus beneficios en múltiples ámbitos.
Beneficios de los que seguramente ya disfrutas en este momento, pues el cálculo está presente en la fabricación de dispositivos electrónicos, muebles, es parte fundamental en la producción de alimentos, etc.
Además, es muy importante en la investigación científica ya que nos permite entender fenómenos como el movimiento de cuerpos celestes, el comportamiento que debe seguir un cohete para ser lanzado al espacio, en fin, no terminaríamos la lista de utilidades que tiene el cálculo, sin embargo, lo más importante es que tu puedes aprenderlo y comprobarlo por ti mismo.
Y en este punto es probable que no te sientas convencido de poder aprenderlo, quizás es la primera vez que lo vas a estudiar y pienses que no estas listo para entender el cálculo porque no confías en lo que aprendiste en algebra, trigonometría y demás conocimientos previos.
O quizás ya has tomado algunas clases y no tuviste la mejor experiencia al intentar aprender, pero no te preocupes, que lo único que necesitas para aprenderlo es una buena y detallada explicación de los temas para aclarar tus dudas, un poco de repaso en los conocimientos previos que se vayan necesitando en cada tema y disciplina.
Nosotros nos encargaremos de traerte toda la información que necesitas, ahora solo depende que dediques unas cuantas horas a la semana según tus objetivos y tiempo disponible. ¡Así que comencemos a hablar de los primeros conceptos que necesitaras!
Definición
El cálculo es la rama de las matemáticas que parte del estudio de tres problemas principales: los problemas de máximos y mínimos, el cálculo de la tangente a una curva y el cálculo del área encerrada bajo una curva. Continuando en la actualidad con el estudio de los cambios y el movimiento.
Siendo así dos ramas del cálculo:
El cálculo diferencial que se encarga del estudio de problemas relacionados con valores máximos y mínimos, y el cálculo de la tangente a una curva.
El cálculo integral que se enfoca en el estudio de problemas relacionados al cálculo del área encerrada bajo una curva.
Etimología
Cálculo es una palabra proveniente del latín “calculus” que significa piedra o piedrecita y está estrechamente relacionada con la palabra calcular del latín “calculare” que significa contar usando piedras, pues los romanos usaban piedras para enseñar a los niños a contar.
Así como ha ocurrido a lo largo de la historia de la humanidad, al emplear distintos objetos para aprender y enseñar a contar, siendo las piedras uno de los elementos más comunes para este fin.
Los conceptos que debes repasar en este momento
Como has leído en este artículo, en cálculo vamos a estar trabajando con funciones durante todo el curso, por lo que consideramos oportuno poner a tu disposición los siguientes conceptos que necesitaras:
Conjunto: es un grupo de objetos denominados como elementos, los cuales comparten características o propiedades semejantes.
Relación: está dada por la correspondencia que existe entre los elementos de dos conjuntos X y Y que forman pares ordenados, mediante la formulación de una expresión que determina su correspondencia.
Ejemplo: siendo un conjunto de frutas y un conjunto de colores, su relación estaría dada por la expresión “el color es”. Donde podemos observar que un elemento del conjunto de frutas puede tener más de una relación con los elementos del conjunto de los colores.
Función: Es una correspondencia dada entre dos conjuntos de números reales, “X” y “Y”, donde cada elemento del conjunto “X” puede tener una relación solo con uno de los elementos del conjunto “Y”.
Por tanto, todas las funciones son relaciones, pero no todas las relaciones son funciones, ya que debe cumplirse que para todo elemento del conjunto “X” debe existir una y solo una relación con algún elemento del conjunto “Y”. Siendo el conjunto “Y” representado como f(x) (se lee f de x).
Esto quiere decir que los elementos del conjunto “Y” están en función de los elementos del conjunto “X”.
Dominio: son todos los valores que puede tomar una función f(x) y para los cuales está definida. El conjunto X en este caso, siendo sus elementos variables independientes.
Rango: Son todos los valores que puede tomar la función. También conocido como imagen de la función o contradominio, el conjunto de las Y en este caso, siendo sus elementos variables dependientes.
Ejemplo 1: Dada la función
donde su dominio esta determinado por cualquier valor de los números reales, mientras que su imagen esta dada por los números positivos. Para obtener su gráfica vamos sustituyendo valores en X para obtener pares ordenados que nos permitan trazar la función.
Ejemplo 2: Dada la función f(x) = donde el dominio puede ser cualquier valor de los números reales excepto el 2, pues
y por tanto la función no está definida para este valor, ya que cuando los valores del dominio se acercan a 2 sus valores en la imagen tienden a
(se lee "más menos infinito").
Ya que llegaste hasta aquí, cuéntanos ¿Qué te ha parecido este articulo?
Somos un blog que busca ayudar a las personas que quieran o necesiten aprender Cálculo en primer lugar, pero también tenemos la intención de fomentar a los lectores el interés por esta rama de las matemáticas pues estamos convencidos de que es más útil de lo que crees.
Coméntanos: ¡Nos interesa tu opinión!