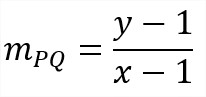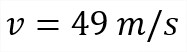En este articulo te mostraremos como surgen los limites cuando tratamos de encontrar la tangente a una curva o la velocidad de un objeto.
El problema de la recta tangente a una curva
Consideramos importante partir de algunos conceptos básicos que nos ayudaran a abordar este tema.
Recta secante: es una recta que interseca (corta) a una curva en más de un punto. Su etimología proviene del latín “secare” (palabra homónima del latín “secans”) que significa cortar.
Y ¿Qué es la tangente?, bueno este concepto es un poco más complejo ya que si hablamos de la tangente a una circunferencia quedaría definida como:
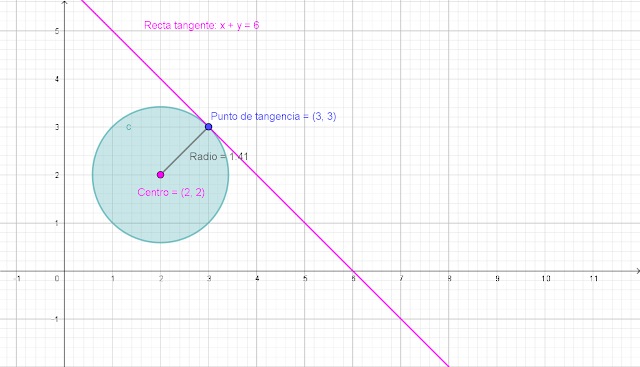
La tangente es la recta que interseca a la circunferencia una y solo una vez.
Si bien esta definición resulta suficiente para la circunferencia, es inadecuada para las curvas planas en general, pues existen curvas planas en las cuales una tangente corta a la curva en uno o más puntos diferentes. Por lo que podríamos definir a la recta tangente a una curva de la siguiente manera:
La tangente es una recta secante en la cual la distancia entre dos de sus puntos, Q y P, se reduce a cero y cuya pendiente se pude expresar como el límite de las pendientes de las rectas secantes que se producen cuando los puntos, Q y P, reducen su distancia entre sí y se acercan a cero.
Como podemos darnos cuenta, esta definición es un poco más difícil de comprender que la anterior, así que creemos oportuno mostrar a detalle esta definición.
Sea la ecuación de una curva plana cualquiera H
Sean P (x1, y1) y Q (x2, y2) dos puntos diferentes cualesquiera de H tales que el arco de la curva que los une sea continuo; es decir, Q puede moverse hacia P permaneciendo siempre sobre la curva. La recta que pasa por P y Q se llama secante.
Consideremos que P es un punto fijo mientras que Q se mueve a lo largo de H hacia P.
Entonces, a medida que Q se aproxima a P, la secante gira en el sentido contrario de las manecillas de un reloj en torno a P y, en general, tiende a una posición límite representada por la recta PF que se define como la tangente a la curva H en el punto P.
El punto P se llama punto de tangencia o punto de contacto de la tangente. La pendiente de la curva H en el punto P se define como la pendiente de la tangente a H en P.
Para calcular la ecuación de la tangente a una curva dada en un punto particular de la curva, es decir que conocemos un punto, el punto de contacto; por lo tanto, queda por hallar la pendiente de la tangente. La pendiente de la secante PQ es
Si H es una curva cualquiera diferente de una línea recta, el valor de la pendiente (m) varia a medida que Q se aproxima a P. Definiéndose la tangente PF como la posición límite de la secante PQ a medida que Q tiende a P, se sigue que la pendiente m de la tangente es el valor límite de la pendiente m dado por
Y escribimos
Siempre que, por supuesto, ese límite exista. La determinación, significado y propiedades de este límite son problemas fundamentales del Cálculo infinitesimal.
Y como queremos que comprendas cada concepto a profundidad, no nos puede faltar darte a conocer su etimología. La palabra tangente proviene del latín “tangens-entis”, que toca. Quien a su vez es el participio presente del verbo “tango-is-ere-tetigi-tactum”, tocar, palpar.
Ejemplo: Encuentre la ecuación de la recta tangente a la parábola
en el punto P(1,1).
Elija
De manera que
Entonces
Por ejemplo, para el punto Q(1.5, 2.25), tenemos que
Las siguientes tablas
muestran los valores de la pendiente de la recta PQ para varios valores de x cercanos a 1. Cuanto más cerca está el punto Q de P, la x es más cercana a 1 y la pendiente de la recta PQ está más cerca de 2.
Esto nos sugiere que la pendiente de la recta tangente T debe ser m=2.
Y, por tanto, podemos decir que la pendiente de la recta tangente es el límite de las pendientes de las rectas secantes, y esto lo expresaremos de la siguiente forma
Y
Suponiendo que la pendiente de la recta tangente finalmente es 2, utilizaremos la ecuación de la recta en la forma punto-pendiente
Para escribir la ecuación de la recta tangente en (1,1) como
O
El problema de la velocidad
El problema de intentar calcular la velocidad de algún objeto, persona, animal, etc., que podemos encontrar en nuestra vida cotidiana, es que no tienen una velocidad constante.
Cuando vemos pasar a una persona en bicicleta esta no se mueve con la misma velocidad durante todo el trayecto, por lo que para abordar este problema calcularemos la velocidad instantánea, ya que como mencionamos la velocidad de los objetos de estudio suele ser variable.
Pero ¿Qué es la velocidad instantánea?
Podemos definir a la velocidad instantánea como el límite de la velocidad promedio cuando el intervalo cuando el intervalo considerado tiende a 0. Y también la definiremos como la derivada del vector de posición respecto al tiempo.
Ambas definiciones son relevantes en términos del cálculo. Además, podemos expresarla matemáticamente de la siguiente forma:
Donde:
Es el vector de la velocidad instantánea. El cual se mide en metros por segundo (m/s).
Es el vector de la velocidad promedio. El cual se mide en metros por segundo (m/s).
Es el vector de desplazamiento. El cual se mide en metros (m).
Es el intervalo de tiempo que tiende a 0, esto es, un intervalo infinitamente pequeño. El cual se mide en segundos (s).
Adicionalmente la palabra velocidad proviene del latín “velocitas”, que significa, cualidad de rápido (etimología).
Ejemplo: Supongamos que dejamos caer una pelota desde la plataforma superior de observación de la Torre CN en Toronto, a 450 m sobre el suelo. ¿Cuál será la velocidad de la pelota después de 5 segundos?
Si buscamos la solución por medio de aproximaciones al límite de la velocidad media tendríamos lo siguiente.
Solución: Mediante experimentos llevados a cabo hace cuatro siglos, Galileo descubrió que la distancia que recorre cualquier cuerpo en caída libre es proporcional al cuadrado del tiempo que ha estado cayendo (modelo que es válido siempre que se desprecie la resistencia del aire).
Si la distancia de caída después de t segundos se denota por
Y se mide en metros, entonces la ley de Galileo se expresa por la ecuación
La dificultad para que encontremos la velocidad después de 5 s es que corresponde a un solo instante de tiempo (t = 5), por lo que no contamos con un intervalo de tiempo.
No obstante, nos podemos aproximar al instante que buscamos mediante el cálculo de la velocidad promedio en el breve intervalo de tiempo de una décima de segundo, desde t = 5 hasta t = 5.1:
En la siguiente tabla te mostramos los resultados de cálculos similares de la velocidad promedio durante periodos cada vez más pequeños.
Como podemos observar, a medida que se acorta el período, la velocidad promedio es cada vez más cercana a 49 m/s.
Por lo tanto, la velocidad instantánea cuando t = 5 queda definida como el valor límite de estas velocidades promedio, durante períodos cada vez más cortos que comienzan en t = 5. De esta forma, la velocidad instantánea después de 5 segundos es
Como te habrás dado cuenta, los cálculos que utilizamos en la solución de este problema son muy similares a los utilizados anteriormente para calcular tangentes.
Ya que hay una estrecha conexión entre el problema de obtener la tangente y aquel de encontrar la velocidad.
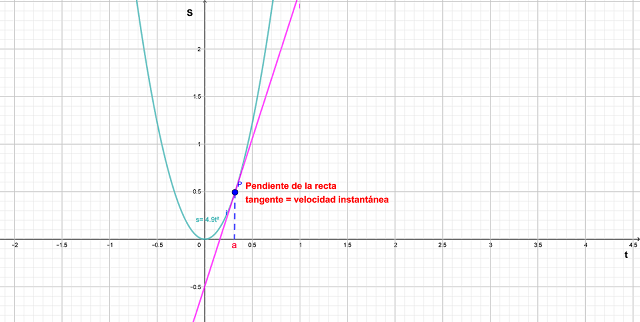
Si dibujamos la gráfica de la función de la distancia recorrida por la pelota
Y consideramos los puntos
Y
Sobre la gráfica, entonces la pendiente de la recta secante PQ es
Que es la misma que la velocidad promedio en el intervalo de tiempo [a, a + h]. Por tanto, la velocidad en el instante t = a (el límite de las velocidades promedio cuando h tiende a 0) debe ser igual a la pendiente de la recta tangente en P (el límite de las pendientes de las rectas secantes).
Como te hemos mostrado en el presente artículo, para que puedas resolver los problemas de la tangente y la velocidad, debes ser capaz de calcular límites.
Sin embargo, abordamos la resolución del límite de una función mediante aproximaciones, el cual, si bien es un método valido y útil, es un tanto laborioso de aplicar.
Por ello en los próximos artículos profundizaremos en los conceptos fundamentales de los límites, te mostraremos técnicas más eficaces a la hora de trabajar con ellos, y finalmente, cuando hayas adquirido estas sólidas bases, te mostraremos un nuevo concepto, la derivada.
Y te preguntaras, ¿para qué me sirve conocer la derivada si ya se un método para resolver problemas de límites? Y la verdad, los beneficios son tantos que muchos de ellos no los entenderías en este momento.
No obstante, te podemos adelantar que aplicando derivadas puedes resolver los ejercicios planteados en este artículo en menos de un minuto y sin tener que escribir tantos procedimientos. Así que continúa leyendo nuestros próximos artículos para que puedas desarrollar estas habilidades.
Recomendaciones
Ya que llegaste hasta aquí, cuéntanos ¿Qué te ha parecido este articulo?
Somos un blog que busca ayudar a las personas que quieran o necesiten aprender Cálculo en primer lugar, pero también tenemos la intención de fomentar a los lectores el interés por esta rama de las matemáticas pues estamos convencidos de que es más útil de lo que crees.
Coméntanos: ¡Nos interesa tu opinión!